Bosco: A tool for automatically conducting doubling experiments for list-based Python functions
Overview and Introduction
Introducing Bosco: a versatile benchmarking framework designed to evaluate the performance of arbitrary list-processing algorithms through doubling experiments. The toolβs name, bosco stands for, Benchmarking of Sorting & Computational Operations. Bosco automates the process of benchmarking by accepting Python source code files containing list-processing functions, fully-qualified function names for benchmarking, and input generation procedures. Leveraging Typer for a user-friendly command-line interface and Poetry for dependency management, Bosco streamlines the benchmarking process. Key features include automatic extraction and invocation of list-processing functions, generation of data sets for doubling experiments, and computation of doubling ratios to infer worst-case time complexity. Diagnostic data, including execution times for each experiment round and inferred time complexities, are provided for comprehensive analysis. With Bosco, researchers and developers can efficiently assess the performance of list-processing algorithms, facilitating informed decision-making and optimization efforts.
Tool Use
To utilize the Bosco tool effectively, navigate to the main directory of your project and execute the tool using a command similar to poetry run bosco --starting-size 100 --number-doubles 5 --file bosco/sorting.py --function-name bubble_sort. This command initiates the benchmarking process with specified parameters: --starting-size determines the initial size of the data set for the doubling experiment, --number-doubles defines how many times the input size will be doubled, --file specifies the path to the file containing the sorting algorithm to test, and --function-name indicates the name of the sorting function within the file.
Once executed, Bosco fetches the results and displays them in a tabular format, showcasing the performance metrics for different input sizes and cases. The output includes the best case, worst case, and average case execution times for each input size during the doubling experiment. Additionally, Bosco generates a graphical representation of the performance data, aiding in visualizing the efficiency of the sorting algorithm under analysis. By following this workflow and interpreting the output, users can gain valuable insights into the computational efficiency of their sorting algorithms and make informed decisions about algorithm selection and optimization strategies. This is an example of the output:
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: quick_sort
Starting size of the data container: 100
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 100 β 0.00058 β 0.00061 β 0.00060 β
β 200 β 0.00129 β 0.00155 β 0.00139 β
β 400 β 0.00268 β 0.00374 β 0.00305 β
β 800 β 0.00578 β 0.00656 β 0.00610 β
β 1600 β 0.01312 β 0.01414 β 0.01372 βFunction Explanation
In our code analysis, several functions stand out for their crucial roles in creating benchmarking experiments and assessing algorithm performance. For example, the generate_random_container function generates randomized data sets essential for benchmarking, it creates a list of integers within a specified range, enabling testing scenarios.
def generate_random_container(size: int) -> List[int]:
"""Generate a random list defined by the size."""
random_list = [random.randint(1, size * size) for _ in range(size)]
return random_listMeanwhile, the run_sorting_algorithm function executes sorting algorithms and profiles their performance using the timeit package. With a call, it measures the execution time of sorting algorithms, providing valuable insights into their efficiency.
def run_sorting_algorithm(file_path: str, algorithm: str, array: List[int]) -> Tuple[float, float, float]:
"""Run a sorting algorithm and profile it with the timeit package."""
directory, file_name = os.path.split(file_path)
module_name = os.path.splitext(file_name)[0]
if directory:
sys.path.append(directory)
try:
module = __import__(module_name)
algorithm_func = getattr(module, algorithm)
except (ImportError, AttributeError):
raise ValueError(f"Could not import {algorithm} from {file_path}")
stmt = f"{algorithm_func.__name__}({array})"
times = repeat(
setup=f"from {module_name} import {algorithm}",
stmt=stmt,
repeat=3,
number=10,
)
return min(times), max(times), sum(times) / len(times)The bosco function serves as the command-line interface for configuring benchmarking experiments. By specifying parameters like the starting size and number of doubles, users can tailor experiments to their needs.
def bosco(starting_size: int = typer.Option(100), number_doubles: int = typer.Option(5),
file: str = typer.Option("./bosco/sorting.py"), function_name: str = typer.Option("bubble_sort")) -> None:
"""Conduct a doubling experiment to measure the performance of list sorting for a specific algorithm."""Additionally, the benchmark module offers utilities for conducting doubling experiments, creating the performance evaluation. The sorting module contains implementations of various sorting algorithms, such as bubble sort and merge sort, enabling comparative analysis. Together, these functions allow for the efficiency of sorting algorithms in different scenarios.
Analysis of outputs from sorting.py
sorting algorithm: bubble_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name bubble_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: bubble_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.05264 β 0.05544 β 0.05364 β
β 1000 β 0.23544 β 0.23749 β 0.23621 β
β 2000 β 0.98467 β 0.99078 β 0.98816 β
β 4000 β 4.07717 β 4.13256 β 4.10616 β
β 8000 β 18.14669 β 19.45909 β 18.70256 βThe first function we evaluated from sorting.py was bubble_sort. The graph shows the best case the worst case and the average case. Each line represents a different case. The average case is the case that will most accurately represent the expected worst case time complexity. The best case, average case, and worst case lines all begin to divided from each other when the input size reaches 4000. It would be interesting to see what factors impact where those lines begin to diverge from each other. Most likely this will change based on the function. One possible avenue of further research could be to look at were those lines diverge. We expected that bubble_sort has a worst case time complexity of \(O(n^2)\). The empirical results, which we see represented with a visual aid in the graph confirm that the worst case time complexity is \(O(n^2)\).
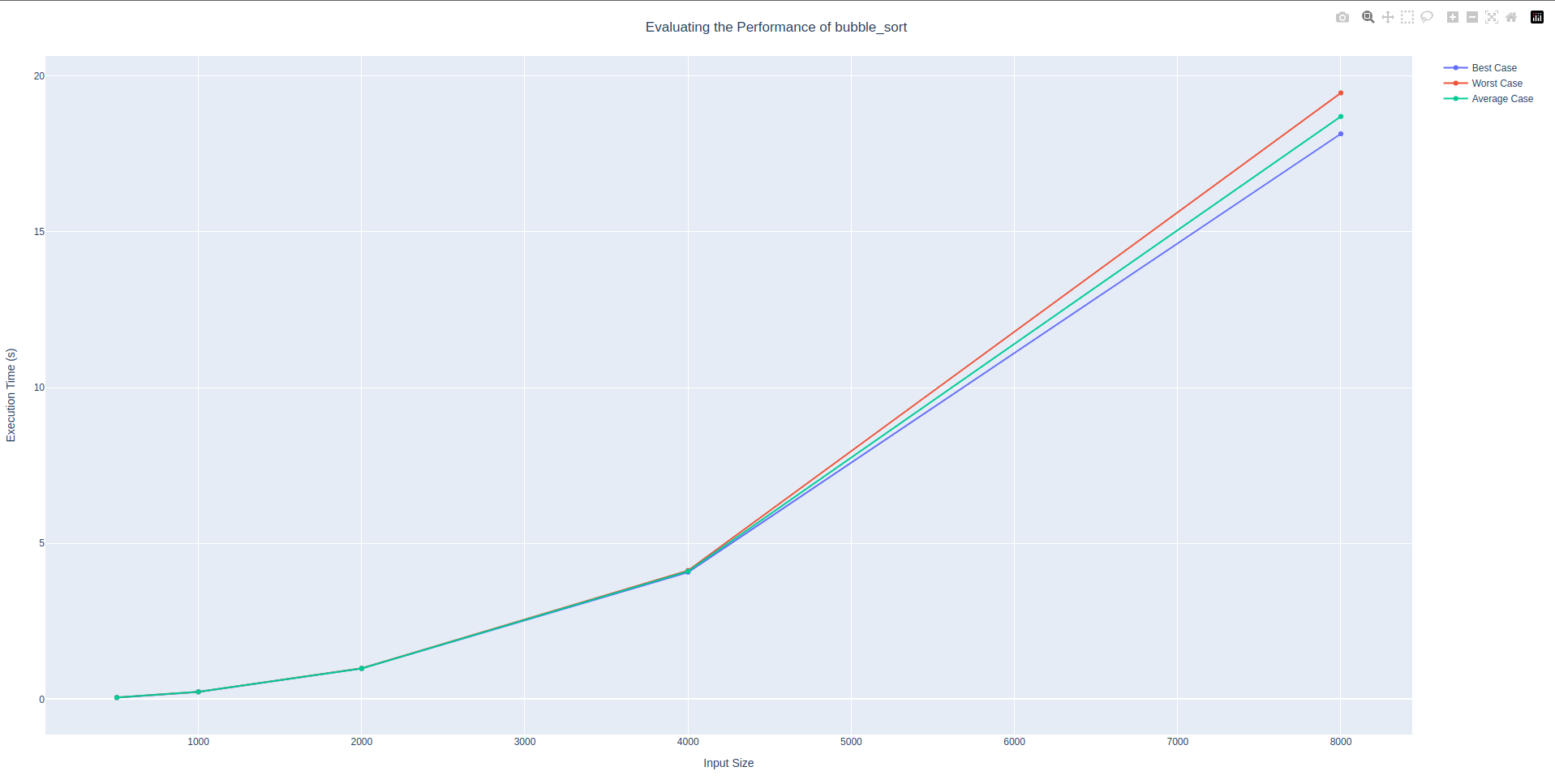
bubble_sort algorithmsorting algorithm: insertion_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name insertion_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: insertion_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.02265 β 0.02386 β 0.02306 β
β 1000 β 0.09508 β 0.11398 β 0.10341 β
β 2000 β 0.40438 β 0.41893 β 0.41121 β
β 4000 β 1.63956 β 1.67517 β 1.66051 β
β 8000 β 6.82943 β 6.88829 β 6.85718 βSimilar to bubble sort there was not a large distance between the best and worst case time results. They were all quite similar. The expected worst case time complexity of this table is \(O(n^2)\). The experimental results confirm the expected worst case time complexity. The values are increasing exponentially. The starting times for the insertion sort function start smaller than the starting values for the bubble sort function.
sorting algorithm: merge_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name merge_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: merge_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00548 β 0.00596 β 0.00572 β
β 1000 β 0.01257 β 0.01346 β 0.01299 β
β 2000 β 0.02722 β 0.02861 β 0.02775 β
β 4000 β 0.06143 β 0.06447 β 0.06278 β
β 8000 β 0.13366 β 0.13735 β 0.13528 βMerge sort started a whole decimal place smaller than both insertion sort and bubble sort. It also had a different worst case time complexity. The worst case time complexity of merge sort was more logarithmic. And its worst-case time complexity was \(O(n \times log_2(n))\). Compared to bubble sort and insertion sort the growth of this function was a bit slow. Which makes sense that it had shorter run times.
While bubble sort approximately had a value of \(0.05\) and insertion sort start at \(0.02\), merge sort started at approximately \(0.005\). However the expected worst case time complexity was still \(O(n^2)\) which was the same as both insertion sort and bubble sort. This shows that although functions can have the same big-O notation and expected worst case time complexity. The empirical results of running the function can still vary a broad amount. So although a function might have a bad big-O notation it is important to consider the time differences that still exist between functions with the same big-O notation.
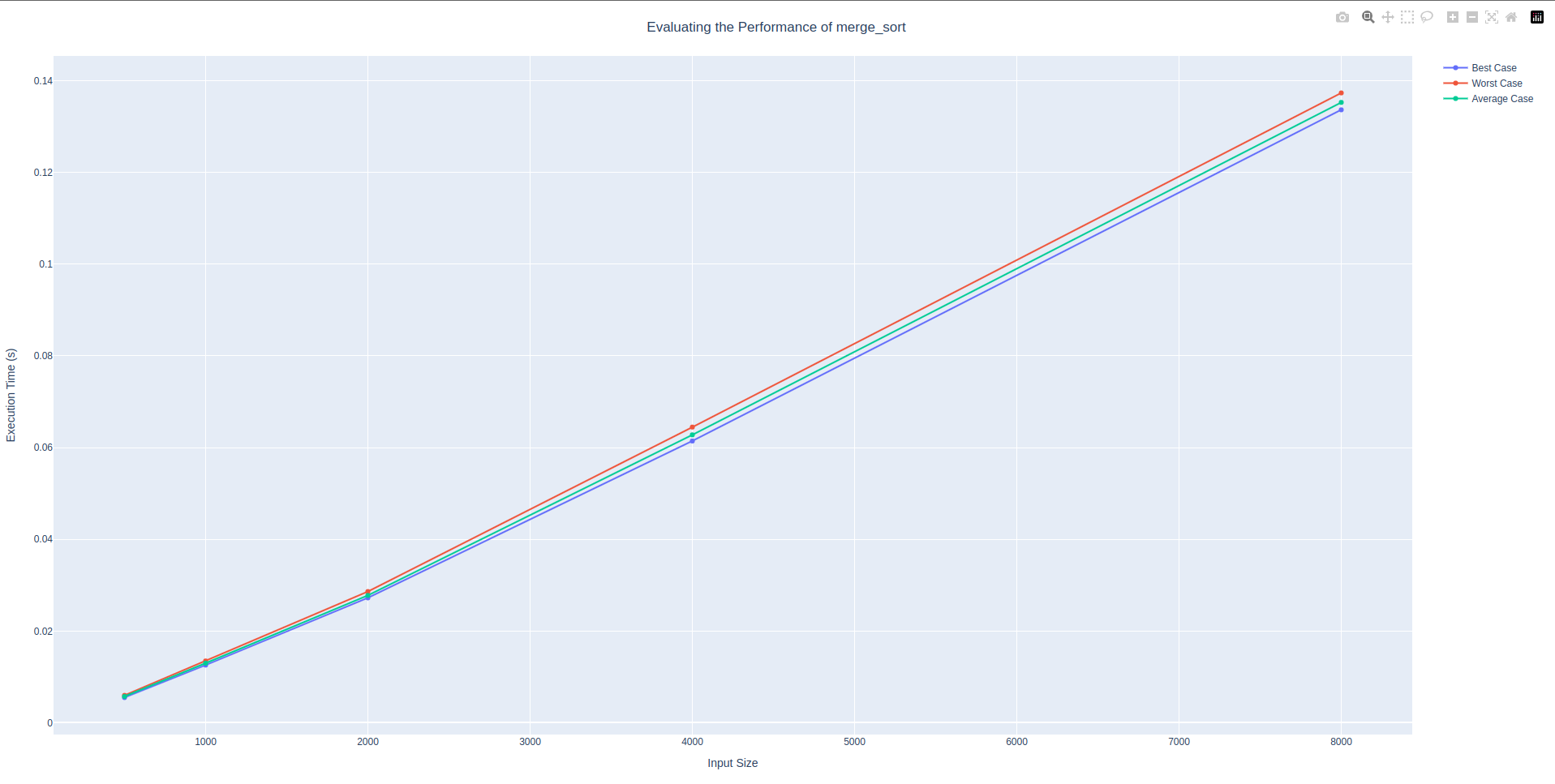
merge_sort algorithmsorting algorithm: quick_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name quick_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: quick_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00340 β 0.00381 β 0.00355 β
β 1000 β 0.00749 β 0.00838 β 0.00802 β
β 2000 β 0.01576 β 0.01692 β 0.01626 β
β 4000 β 0.03622 β 0.03649 β 0.03637 β
β 8000 β 0.07017 β 0.07449 β 0.07220 βIn contrast to insertion sort and bubble sort and similarly to merge sort quick sort also had a \(O(n \times log_2(n))\) expected worst case time complexity. Quick sort had a tinier run time than merge sort. It started at a value of \(0.003\) whereas merge sort started with a value of \(0.005\).
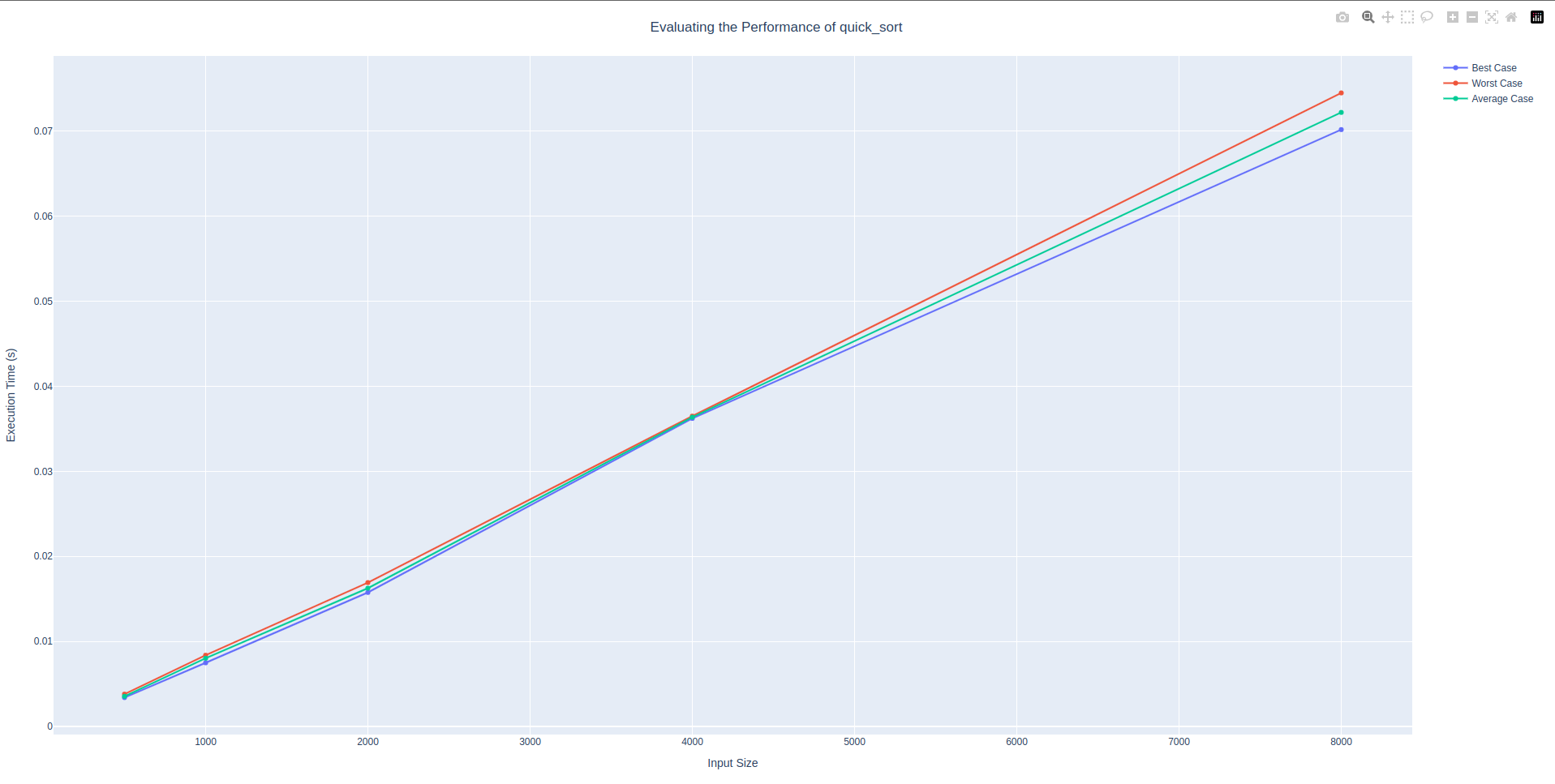
quick_sort algorithmsorting algorithm: tim_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name tim_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: tim_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00408 β 0.00441 β 0.00421 β
β 1000 β 0.01001 β 0.01021 β 0.01011 β
β 2000 β 0.02154 β 0.02382 β 0.02267 β
β 4000 β 0.04829 β 0.04948 β 0.04881 β
β 8000 β 0.10955 β 0.11133 β 0.11039 βTim sort also had an expected worst case time complexity of \(O(n \times log_2(n))\). The empirical results corroborate this. The data clearly shows that the results close to double every run. This shows that the worst case time complexity is indeed linearithmic
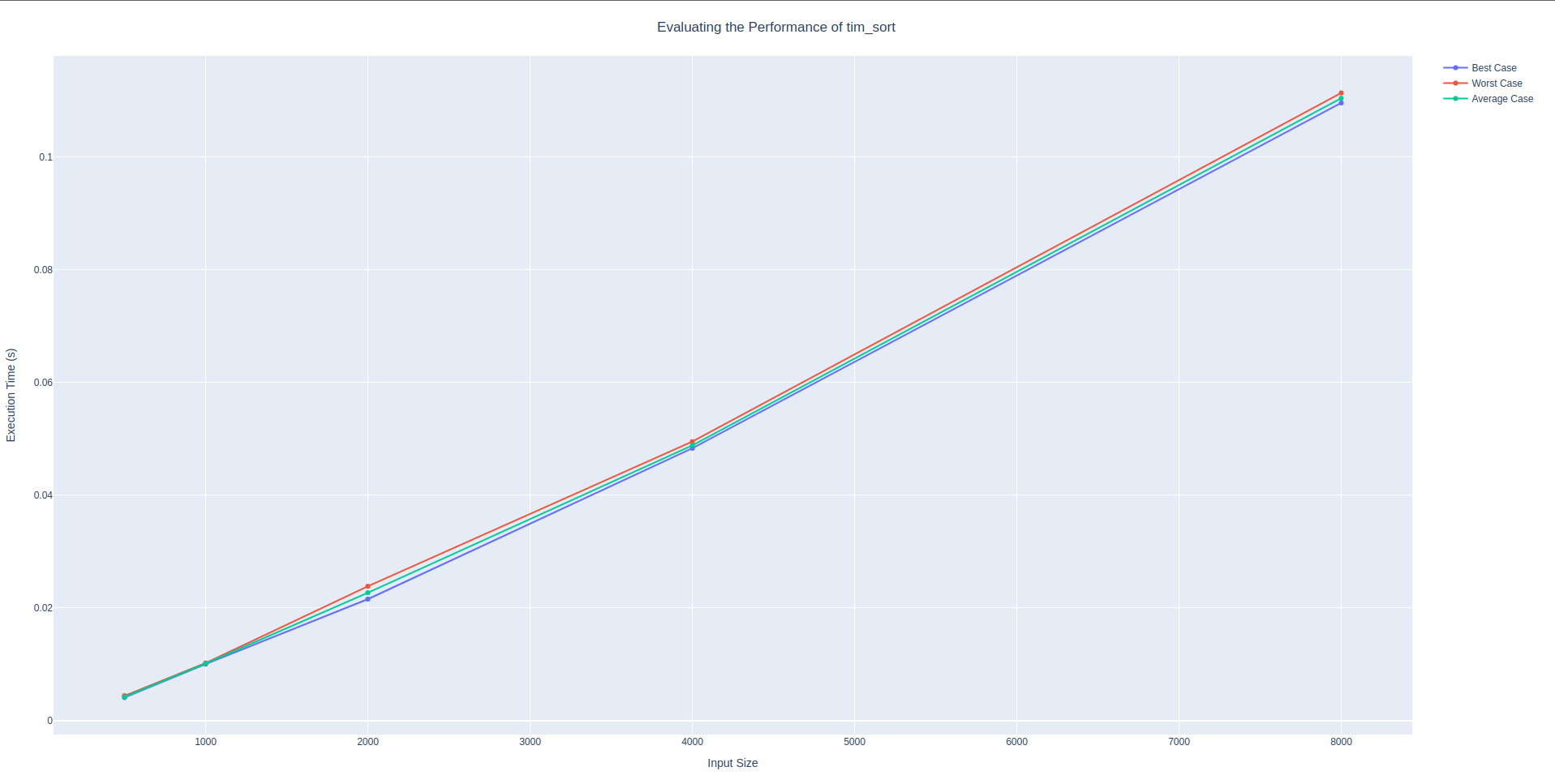
tim_sort algorithmsorting algorithm: selection_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name selection_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: selection_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.02625 β 0.02953 β 0.02776 β
β 1000 β 0.10975 β 0.11727 β 0.11361 β
β 2000 β 0.42805 β 0.44667 β 0.43990 β
β 4000 β 1.72169 β 1.73033 β 1.72708 β
β 8000 β 7.01161 β 7.44163 β 7.19390 βThus far, selection sort also has one of the slower run times and shows that it doubles quite quickly, though not as quick as bubble sort. By the end of the 5th run the bubble sort program had a worst case runtime of \(18\) seconds. Though selection sort wasnβt as fast as merge sort or tim sort, neither was it as slow as bubble sort and it was \(0.2\) seconds away from insertionβs sort worst case of \(6.8\). Selection sort also had a worst case time complexity of \(O(n^2)\) and had timed results most similar to that of insertion sort.
sorting algorithm: heap_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name heap_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: heap_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00553 β 0.00626 β 0.00584 β
β 1000 β 0.01294 β 0.01332 β 0.01310 β
β 2000 β 0.02856 β 0.02947 β 0.02910 β
β 4000 β 0.06260 β 0.06543 β 0.06408 β
β 8000 β 0.13563 β 0.13867 β 0.13718 βHeap sort appears to be another logarithmic function. It results are close to doubling on every iteration of the doubling experiment. As the input size doubles, we can see this functions results are also close to doubling though they are not exactly doubling.
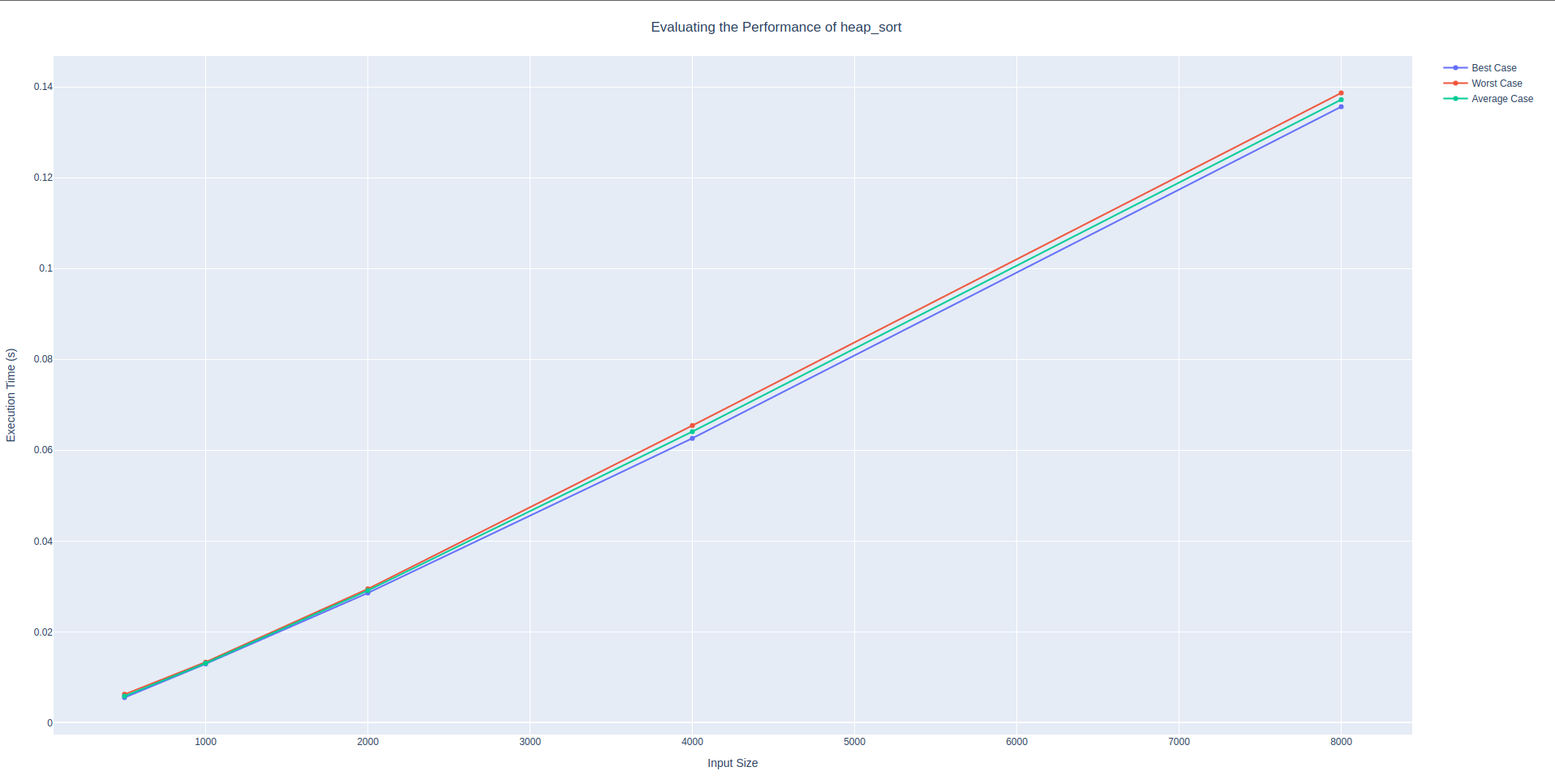
heap_sort algorithmsorting algorithm: shell_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name shell_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: shell_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00314 β 0.00452 β 0.00372 β
β 1000 β 0.00777 β 0.00834 β 0.00802 β
β 2000 β 0.01915 β 0.02002 β 0.01953 β
β 4000 β 0.04701 β 0.04802 β 0.04757 β
β 8000 β 0.10575 β 0.11186 β 0.10789 βIn addition to heap sort this also appears to be a logarithmic function. The results go from 0.004, to 0.008 almost a perfect double. Then from 0.008 to 0.020 which is pretty close to a double though it is a little more and a double. The next run goes from 0.02 to 0. 04 which again is doubling. However, we see the difference between the fourth and the fifth run take a bigger spike. The number between these runs go from 0.04 to 0.11 which is almost tripling. This shows that it isnβt linear though from the first four runs it might have been able to think that. The fourth to the fifth run indicate to us that this is more than linear, and this is where the logarithmic part of the big-O notation come into play.
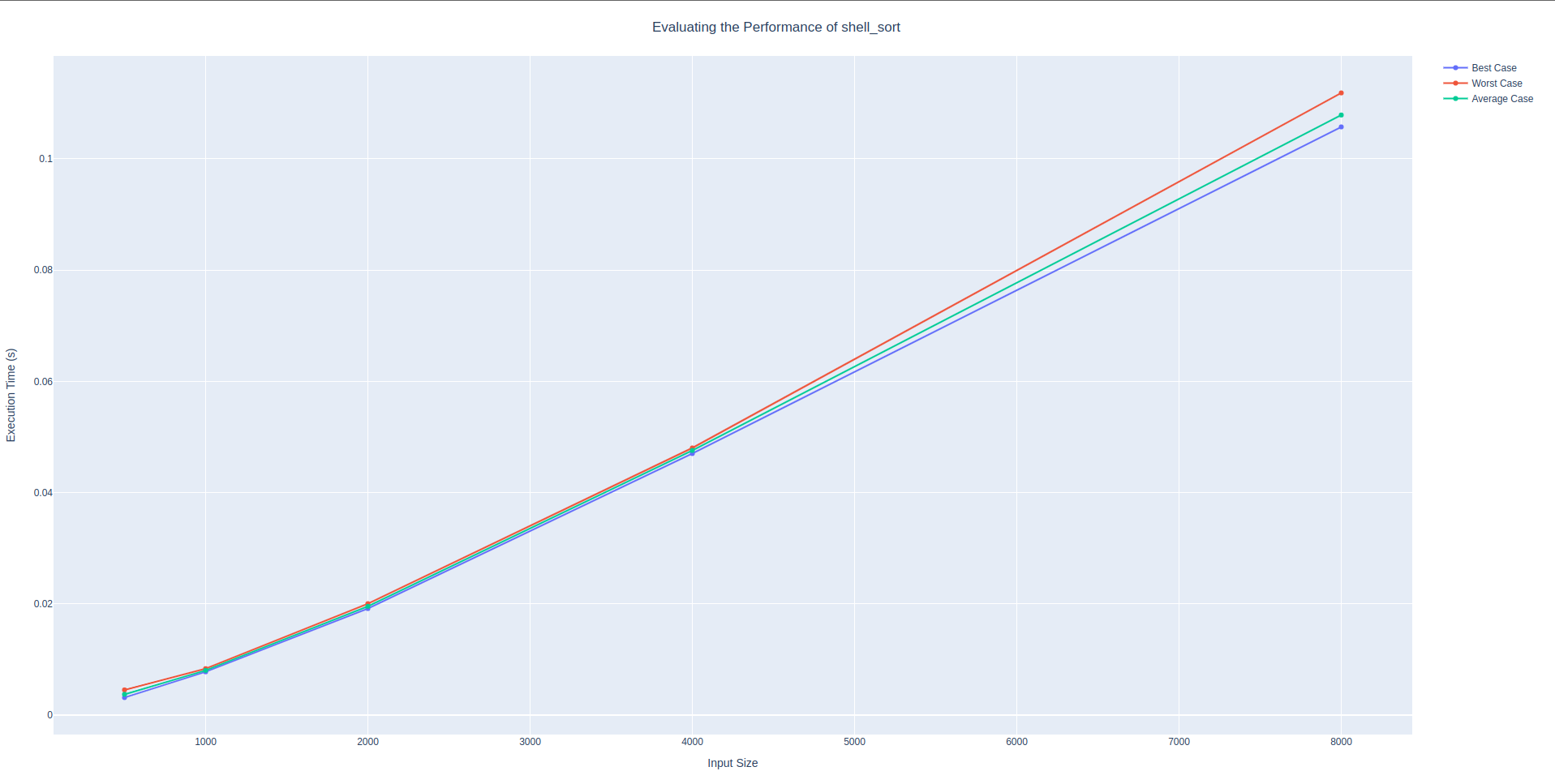
shell_sort algorithmsorting algorithm: radix_sort
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name radix_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: radix_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.00552 β 0.00561 β 0.00555 β
β 1000 β 0.01072 β 0.01110 β 0.01089 β
β 2000 β 0.02427 β 0.02509 β 0.02472 β
β 4000 β 0.05889 β 0.06040 β 0.05962 β
β 8000 β 0.11634 β 0.12265 β 0.11910 βRadix sort also appears linear for the first three runs. However, in contrast to shell sort radix sort begins to more than double between the third and fourth runs, whereas we saw this change in the shell sort function between runs four and five. Here, run three has a value of 0.024 and run four has a value of 0.059. This is more than doubled, though it is still under tripling. The next run from four to five appears much closer to a double. This inconsistency probably has to do with the small data sizes. In order to get more information it would be prudent to increase the input size and see how long it take before this sorting algorithm takes to long to calculate the next iteration of the function. Ways to do this will be discussed further in the future work section of this article.
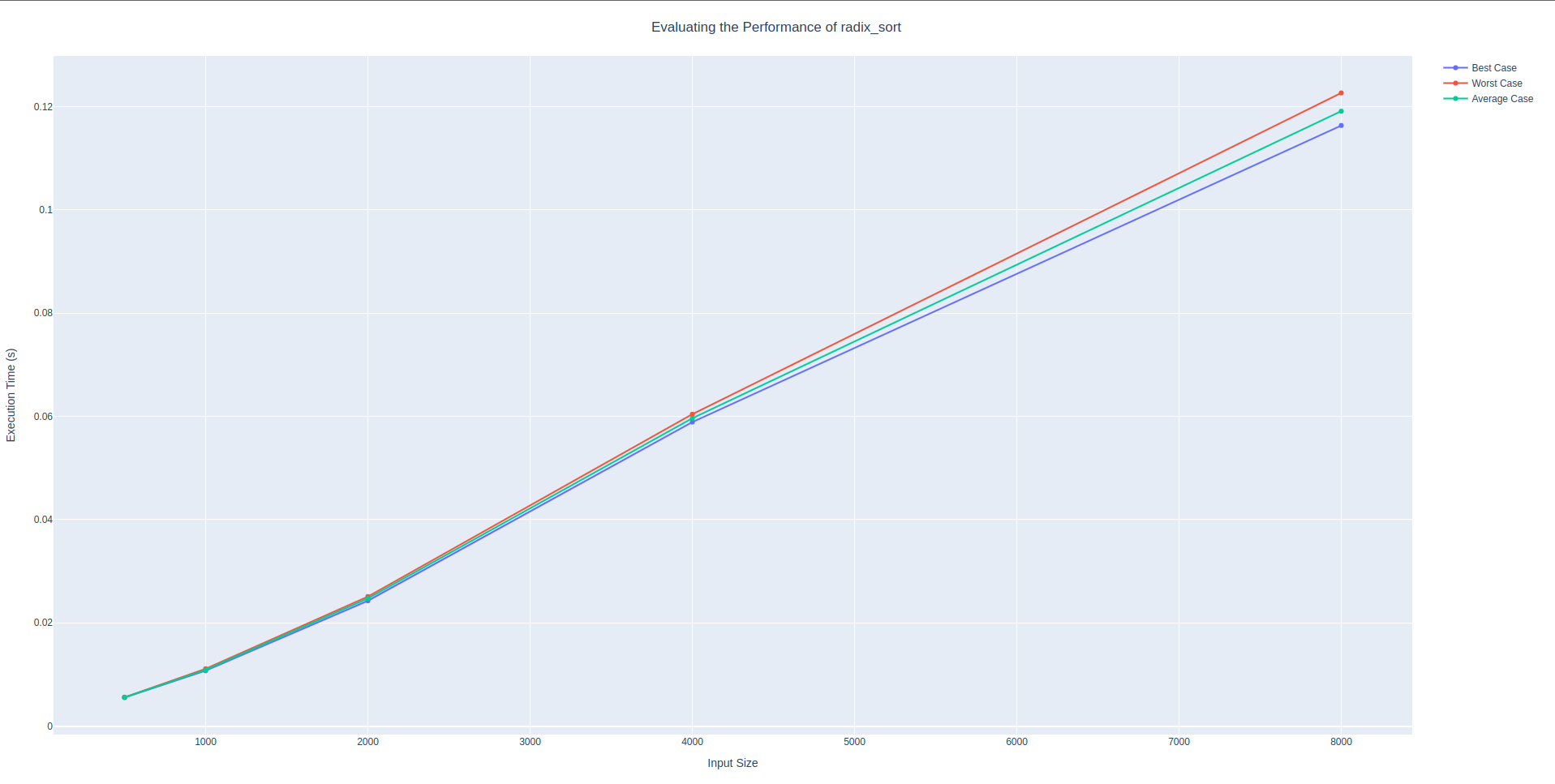
radix_sort algorithmSorting algorithm: bucket_sortGraph
Command: poetry run bosco --starting-size 500 --number-doubles 5 --file bosco/sorting.py --function-name bucket_sort
πΆ Bosco is fetching our results!
Path to the desired file: bosco/sorting.py
Name of the desired function: bucket_sort
Starting size of the data container: 500
Number of doubles to execute: 5
π Here are the results from running the experiment!
β Input Size β Best Case β Worst Case β Average Case β
β 500 β 0.02477 β 0.02569 β 0.02529 β
β 1000 β 0.10665 β 0.10891 β 0.10806 β
β 2000 β 0.43654 β 0.45832 β 0.44521 β
β 4000 β 1.79721 β 1.83186 β 1.81489 β
β 8000 β 7.18055 β 8.15643 β 7.63618 βBucket sort has a worse worst case time complexity than logarithmic. This is clear from the data because the data more than doubles on every run, starting from the beginning. Between runs \(14\) and \(2\) the time jumps from \(0.025\) to \(0.10\). This is just over tripling in time spent. This trend continues through out the rest of the function. The next jump that is made is from \(0.10\) to \(0.44\).
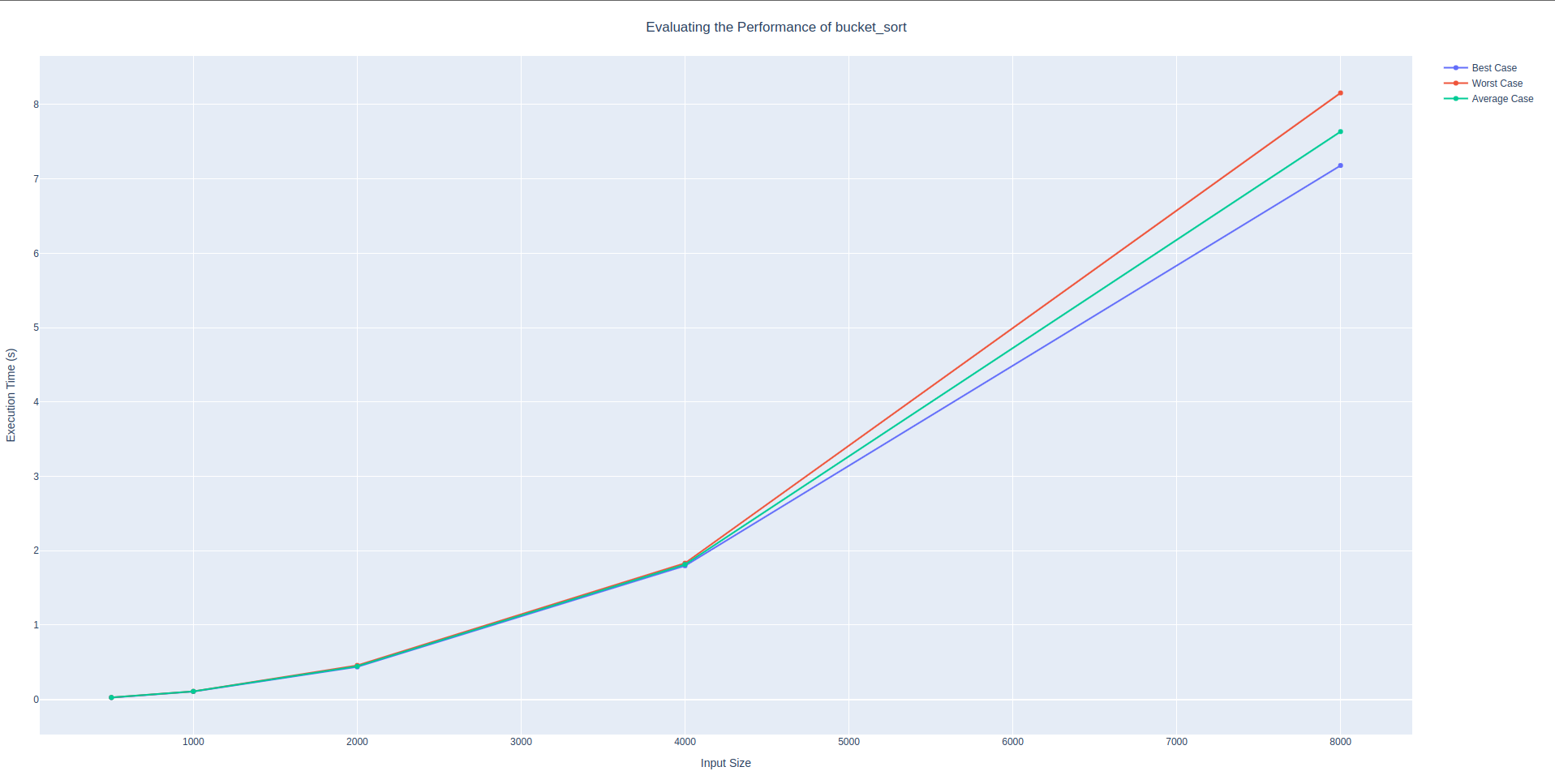
bucket_sort algorithmConclusion
Overall, along with bubble_sort there are many other function that also show a worst case time complexity of \(O(n^2)\). Not limited to, but including, selection sort and insertion sort. Bubble sort, selection sort, and insertion sort all had a estimated worst case time complexities of \(O(n^2)\). While quick sort and merge sort had estimated worst case time complexities of \(O(n \times log_2(n))\). These result were also corroborated by the βDoubling Experiment with O(n) Analysisβ All-Hands project and the βSimple sorting algorithm doubling experiment with worst-case time complexity analysisβ All-Hands project. The βComparative analysis of sorting algorithmsβ also found those same results along with analyzing bucket sort which was also \(O(n^2)\) and radix, heap, tim, and merge sort which were more logarithmic. Beyond some of these function there are many more functions in the sorting.py file. Future work could consist of evaluating all those function more closely, along with adding others.
Future Work
In further experimental studies it might be best to adjust the data type of the results. We could make a function that would determine the sizes the runs should be based on the how long the function takes to run the above experiment. Then the computer would determine the number of runs the computer would make in order to get the most data possible. This would also help to push functions to their limits and so it would return the functions in their truly worst case and at their max limit.
One approach to implementing this is to use an if statement to check the time each run took. We could code it so that the run would continue until the float value holding the time reached the max time we set and then the runs would stop. For example, I could specific that I want every function to reach a limit of 30 seconds before it returns the runs. This could even be as simple as implementing a while loop and break the loop and return the already received result to the user. Then there could be a function that would adjust the inputs of the list passed in based on the amount of time it took to run. The computer would repeat this process until it determined the necessary amount of data to give the function based on itβs previous run times, this way the doubling experiments would all be hitting their ceiling and this would better allow us to compare results as algorithm engineers.